Firstly a quick apology for not adding this last night - I was busy writing some fun API examples!
The aim of this Kata is to think about coming up with a pricing model for products in a supermarket that allows you to handle such variations as “3 for 2” (what is the 3rd item’s price?), “3 for £1” (how much is 4?), £2 per kilo (how much is 300g?) and other such pricing variations. I have altered the original Kata slightly to use the metric weight system as well as Sterling currency (more for my own ease – it doesn’t alter the content of the Kata).
My initial thoughts on the walk to work this morning were around creating a “Product” object with which I could associate a number of “Pricing Schemes”. For example:
“I have oranges to sell at 50p each or 5 for £2”
Leading to an object structure as follows:
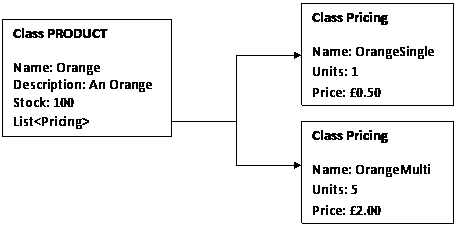
Then when making a purchase of 6 oranges say, our system could perform a modulo operation against the pricing with the highest number of units (here 5) to retrieve a spare of 1. The system could then divide 6 but 5 to return a value greater than 1 thus making a purchase of 5 Oranges for £2 plus an extra orange for 50p giving a total of £2.50.
Now I believe this would solve all of our situations mentioned above (where for the weight example we would work in units compared to the price, so say we have bananas at £2 per kilo, 1 kilo of bananas is 1 unit which means if we by 500grams we then by half a unit of bananas.
The first issues I could see arising however was the following; how do we include items on cross product multi-buy discounts (for example any 5 chocolate bars for £1)? This led me to experiment with the idea of a single product class for each different product with its pricing. So for the Oranges example above, this would be 2 different products with a “parent product” property (of Orange), “number of units” property (of 5 and 1) and a “price” property (of £0.50 and £2.00). This however also has restrictions as we are unlikely to be able to inherit from multiple parents classes in our language.
We can abandon this idea however but to solve our problem come up with a different way of dealing with cross product multi-buys. This could be for example, having a cross-product offer class that will contain a list of objects it applies to and a pricing overall.
The ideal solution I came up with however would be to have a pricing that was referenced by multiple products in their listing which we could then process at the end of the transaction. This would allow us to have separately dealt with the issue of inventory, not have increased the number of classes required and have simplified the running of the business logic.
** Reflection
The practice of this Kata has helped me to see how despite the many options that are available to us in our design schema, it is preferable to minimise the overall complexity of the class structure whilst at the same time maximising its possible flexibility. This sounds like a fairly obvious statement but one that can often get overlooked as we must try to also be clear enough as to not shoehorn something in “just because we liked the original idea”. I could have easily made the case for any number of different class schemas but it would not have been the schema I was most comfortable working with and therefore would have put me at a disadvantage, thus adding risk to the system.
I think the main learning tip I will take from this is although all nuances and variations need to be accounted for, if you end up being uncomfortable with programming using the schema then it is not the ideal schema for the system.